Приложение для курсовой «Экосистема кроликов и лис»
Содержимое: Vol.rar (294.11 KB)
Загружен: 05.09.2017
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 1
Возвраты: 0
767.52 руб.
В АРХИВЕ ПРЕДСТАВЛЕНА ТОЛЬКО ПРОГРАММА С НЕКОТОРЫМИ ТЕОРЕТИЧЕСКИМИ СВЕДЕНИЯМИ. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА ОТСУТСТВУЕТ!
Вариант 2.7
Рассмотрим простую экосистему, состоящую из кроликов, для которых имеется неограниченный запас пищи, и лис, которые для пропитания охотятся за кроликами. Классическая математическая модель, принадлежащая Вольтерра, описывает эту систему двумя нелинейными уравнениями первого порядка:
dr/dt = 2r -αrf, r (0) = r0,
df/dt=-f + αrf, f(0) = f0.
Здесь t-время, r = r (t) - число кроликов, f = f(t)- число лис и α - поло¬жительная константа. При α = 0 две популяции не взаимодействуют, и кролики делают то, что у кроликов получается лучше всего, а лисы вымирают от голода. При α > 0 лисы встречают кроликов с вероятностью, пропорциональной произведению числа тех и других. В результате таких встреч число кроликов убывает, а число лис (по менее очевидным причинам) возрастает.
Исследуйте поведение этой системы для α = 0.01 и различных значений r0 и f0, простирающихся от 2 или 3 до нескольких тысяч. Нарисуйте графики наиболее интересных решений. Начертите также график с осями r и f. Поскольку мы умалчиваем о единицах измерения, нет причин ограничивать r и f только целыми значениями.
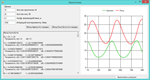
(а)Вычислите решение для r0 = 300 и f0 = 150. Вы должны обнаружить, что поведение системы периодично с периодом, очень близким к 5 единицам времени. Иными словами, r(0) ≈ r(5) и f (0) ≈ f(5).
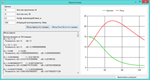
(б)Вычислите решение для r0 = 15 и f0 = 22. Вы должны получить, что число кроликов в конечном счете становится меньше 1. Это можно интерпретировать так, что кролики вымирают. Найдите начальные условия, которые обрекают на вымирание лис. Найдите начальные условия с r0 = f0, при которых вымирают оба вида.
(в)Может ли какая-либо компонента точного решения стать отрицательной? Может ли стать отрицательным численное решение? Что произойдет в этом случае? (На практике ответы на последние два вопроса могут зависеть от заданных вами границ погрешностей.)
(г)Было предложено много модификаций этой простой модели, чтобы более полно отразить то, что происходит в природе. Например, можно воспрепятствовать неограниченному возрастанию числа кроликов, заменив первое уравнение на
dr/dt=2(1-r/R)r-αrf
Теперь даже при α = 0 число кроликов никогда не может превысить R. Выберите какое-либо разумное значение для R и вновь рассмотрите некоторые из поставленных вопросов. В частности, что произойдет с периодичностью решений?
Вариант 2.7
Рассмотрим простую экосистему, состоящую из кроликов, для которых имеется неограниченный запас пищи, и лис, которые для пропитания охотятся за кроликами. Классическая математическая модель, принадлежащая Вольтерра, описывает эту систему двумя нелинейными уравнениями первого порядка:
dr/dt = 2r -αrf, r (0) = r0,
df/dt=-f + αrf, f(0) = f0.
Здесь t-время, r = r (t) - число кроликов, f = f(t)- число лис и α - поло¬жительная константа. При α = 0 две популяции не взаимодействуют, и кролики делают то, что у кроликов получается лучше всего, а лисы вымирают от голода. При α > 0 лисы встречают кроликов с вероятностью, пропорциональной произведению числа тех и других. В результате таких встреч число кроликов убывает, а число лис (по менее очевидным причинам) возрастает.
Исследуйте поведение этой системы для α = 0.01 и различных значений r0 и f0, простирающихся от 2 или 3 до нескольких тысяч. Нарисуйте графики наиболее интересных решений. Начертите также график с осями r и f. Поскольку мы умалчиваем о единицах измерения, нет причин ограничивать r и f только целыми значениями.
(а)Вычислите решение для r0 = 300 и f0 = 150. Вы должны обнаружить, что поведение системы периодично с периодом, очень близким к 5 единицам времени. Иными словами, r(0) ≈ r(5) и f (0) ≈ f(5).
(б)Вычислите решение для r0 = 15 и f0 = 22. Вы должны получить, что число кроликов в конечном счете становится меньше 1. Это можно интерпретировать так, что кролики вымирают. Найдите начальные условия, которые обрекают на вымирание лис. Найдите начальные условия с r0 = f0, при которых вымирают оба вида.
(в)Может ли какая-либо компонента точного решения стать отрицательной? Может ли стать отрицательным численное решение? Что произойдет в этом случае? (На практике ответы на последние два вопроса могут зависеть от заданных вами границ погрешностей.)
(г)Было предложено много модификаций этой простой модели, чтобы более полно отразить то, что происходит в природе. Например, можно воспрепятствовать неограниченному возрастанию числа кроликов, заменив первое уравнение на
dr/dt=2(1-r/R)r-αrf
Теперь даже при α = 0 число кроликов никогда не может превысить R. Выберите какое-либо разумное значение для R и вновь рассмотрите некоторые из поставленных вопросов. В частности, что произойдет с периодичностью решений?
Отзывов от покупателей не поступало