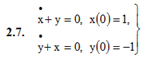DHS 16.2 - Option 7. Decisions Ryabushko AP
Content: 7v-IDZ16.2.pdf (71.96 KB)
Uploaded: 10.07.2025
Positive responses: 0
Negative responses: 0
Sold: 0
Refunds: 0
$0.96
1. Solve a linear differential equation using the operator method
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
The function f(t) and values of coefficients α, β, γ, t0, x(t0), ẋ(t0) are taken from the table. 16.4
1.7. α = 1, β = 0, γ = −9, f(t) = 2 − t, t0 = 0, x(t0) = 0, ẋ(t0) = 1
1.7. ẍ − 9x = 2 − t, x(0) = 0, ẋ(0) = 1
2. Solve the system of linear differential equations by the operator method
Table of functions f1(t), f2(t) and values ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0). 16.5
2.7. a1 = 1, b1 = 0, c1 = 0, d1 = 1, f1(t) = 0, a2 = 0, b2 = 1, c2 = 1, d2 = 0, f2(t) = 0, x(0) = 1, y(0) = −1
αẍ + βẋ + γx = f(t), x(t0) = A, ẋ(t0) = B
The function f(t) and values of coefficients α, β, γ, t0, x(t0), ẋ(t0) are taken from the table. 16.4
1.7. α = 1, β = 0, γ = −9, f(t) = 2 − t, t0 = 0, x(t0) = 0, ẋ(t0) = 1
1.7. ẍ − 9x = 2 − t, x(0) = 0, ẋ(0) = 1
2. Solve the system of linear differential equations by the operator method
Table of functions f1(t), f2(t) and values ak, bk, ck, dk (k=1, 2), A, B, x(0), y(0). 16.5
2.7. a1 = 1, b1 = 0, c1 = 0, d1 = 1, f1(t) = 0, a2 = 0, b2 = 1, c2 = 1, d2 = 0, f2(t) = 0, x(0) = 1, y(0) = −1
Detailed solution. Designed in PDF format for easy viewing of IDZ solutions on smartphones and PCs. In MS Word (doc format) sent additionally.
No feedback yet