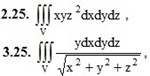ИДЗ 13.2 – Вариант 25. Решения Рябушко А.П.
Содержимое: 25v-IDZ13.2.pdf (83.61 KB)
Загружен: 10.07.2025
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 1
Возвраты: 0
Продавец: Massimo86
информация о продавце и его товарах
Cкидка постоянным покупателям! Если общая сумма ваших покупок у продавца больше чем:
| $3 | скидка | 1% |
| $6 | скидка | 2% |
| $9 | скидка | 3% |
| $12 | скидка | 4% |
| $15 | скидка | 5% |
| $18 | скидка | 6% |
| $20 | скидка | 7% |
| $30 | скидка | 10% |
100 руб.
1. Расставить пределы интегрирования в тройном интеграле если область V ограничена указанными поверхностями. Начертить область интегрирования
1.25. V: x = 2, y ≥ 0, z ≥ 0, y = 3x, z = 4(x2 + y2)
2. Вычислить данные тройные интегралы.
V: 0 ≤ x ≤ 2, −1 ≤ y ≤ 0, 0 ≤ z ≤ 4
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: 4 ≤ x2 + y2 + z2 ≤ 16, y ≤ √3x, y ≥ 0, z ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.25. z ≥ 0, y + z = 2, x2 + y2 = 4
1.25. V: x = 2, y ≥ 0, z ≥ 0, y = 3x, z = 4(x2 + y2)
2. Вычислить данные тройные интегралы.
V: 0 ≤ x ≤ 2, −1 ≤ y ≤ 0, 0 ≤ z ≤ 4
3. Вычислить тройной интеграл с помощью цилиндрических или сферических координат.
, υ: 4 ≤ x2 + y2 + z2 ≤ 16, y ≤ √3x, y ≥ 0, z ≥ 0
4. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
4.25. z ≥ 0, y + z = 2, x2 + y2 = 4
Подробное решение. Оформлено в PDF-формате для удобства просмотра решений ИДЗ на смартфонах и ПК.
В MS Word (doc-формате) высылается дополнительно.
В MS Word (doc-формате) высылается дополнительно.
Отзывов от покупателей не поступало