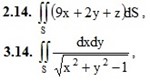ИДЗ 15.1 – Вариант 14. Решения Рябушко А.П.
Содержимое: 14v-IDZ15.1.pdf (120.38 KB)
Загружен: 10.07.2025
Положительные отзывы: 0
Отрицательные отзывы: 0
Продано: 2
Возвраты: 0
120 руб.
1. Дана функция u(M) = u(x, y, z) и точки M1, M2. Вычислить: 1) производную этой функции в точке M1 по направлению вектора M1M2; 2) grad u(M1)
1.14. u(M) = ln(1 + x + y2 + z2), M1(1, 1, 1), M2(3, –5, 1)
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S – часть плоскости (p), отсеченная координатными плоскостями.
(p): 2x + y + z = 4
3. Вычислить поверхностный интеграл второго рода.
где S – часть поверхности гиперболоида x2 + y2 = z2 + 1(нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостями z = 0 и z = √3.
4. Вычислить поток векторного поля a(M) через внешнюю поверхность пирамиды, образуемую плоскостью (p) и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского – Гаусса.
4.14. а(M) = 4xi + (x – y – z)j + (3y + 2z)k, (p): 2x + y + z = 4
1.14. u(M) = ln(1 + x + y2 + z2), M1(1, 1, 1), M2(3, –5, 1)
2. Вычислить поверхностный интеграл первого рода по поверхности S, где S – часть плоскости (p), отсеченная координатными плоскостями.
(p): 2x + y + z = 4
3. Вычислить поверхностный интеграл второго рода.
где S – часть поверхности гиперболоида x2 + y2 = z2 + 1(нормальный вектор n которой образует тупой угол с ортом k), отсекаемая плоскостями z = 0 и z = √3.
4. Вычислить поток векторного поля a(M) через внешнюю поверхность пирамиды, образуемую плоскостью (p) и координатными плоскостями, двумя способами: а) использовав определение потока; б) с помощью формулы Остроградского – Гаусса.
4.14. а(M) = 4xi + (x – y – z)j + (3y + 2z)k, (p): 2x + y + z = 4
Подробное решение. Оформлено в PDF-формате для удобства просмотра решений ИДЗ на смартфонах и ПК.
В MS Word (doc-формате) высылается дополнительно.
В MS Word (doc-формате) высылается дополнительно.
Отзывов от покупателей не поступало