Solution D3-94 (Figure D3.9 condition 4 SM Targ 1989)
Content: d3-94.doc.RAR (24.08 KB)
Uploaded: 26.05.2016
Positive responses: 0
Negative responses: 0
Sold: 1
Refunds: 0
Seller: Михаил_Перович
information about the seller and its items
Loyalty discount! If the total amount of your purchases from the seller more than:
| $1 | the discount is | 1% |
| $5 | the discount is | 2% |
| $10 | the discount is | 3% |
| $20 | the discount is | 5% |
| $50 | the discount is | 7% |
| $100 | the discount is | 10% |
| $200 | the discount is | 15% |
$0.63
Solution D3-94 (Figure D3.9 condition 4 SM Targ 1989)
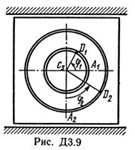
The mechanical system consists of loads D1 of mass m1 = 2 kg and D2 with a mass of m2 = 6 kg and a rectangular vertical plate of mass m3 = 12 kg moving along the horizontal guides (Fig. D3.0 - D3.9, Table D3). At time t0 = 0, when the system was at rest, under the action of internal forces, the loads begin to move along the troughs, which are circles of radii r = 0.4 m and R = 0.8 m.
When the goods move, the angle φ1 = ∠A2C3D1 changes according to the law φ1 = f1 (t), and the angle φ2 = ∠A2C3D2 - according to the law φ2 = f2 (t). In Table. DZ, these dependences are given separately for Fig. 0-4 and 5-9, where φ is expressed in radians, t is in seconds. Considering the loads as material points and neglecting all the resistances, determine the law of the time variation of the value indicated in the table in the "Find" column, ie, x3 = t3 (t) and N = f (t), where x3 is the coordinate of the center C3 of the plate (the dependence x3 = f3 (t) determines the law of motion of the plate), N is the total normal reaction of the guides.
The mechanical system consists of loads D1 of mass m1 = 2 kg and D2 with a mass of m2 = 6 kg and a rectangular vertical plate of mass m3 = 12 kg moving along the horizontal guides (Fig. D3.0 - D3.9, Table D3). At time t0 = 0, when the system was at rest, under the action of internal forces, the loads begin to move along the troughs, which are circles of radii r = 0.4 m and R = 0.8 m.
When the goods move, the angle φ1 = ∠A2C3D1 changes according to the law φ1 = f1 (t), and the angle φ2 = ∠A2C3D2 - according to the law φ2 = f2 (t). In Table. DZ, these dependences are given separately for Fig. 0-4 and 5-9, where φ is expressed in radians, t is in seconds. Considering the loads as material points and neglecting all the resistances, determine the law of the time variation of the value indicated in the table in the "Find" column, ie, x3 = t3 (t) and N = f (t), where x3 is the coordinate of the center C3 of the plate (the dependence x3 = f3 (t) determines the law of motion of the plate), N is the total normal reaction of the guides.
No feedback yet