Solution K3-28 (Figure K3.2 condition 8 SM Targ 1988)
Content: К3-28_1988.rar (33.86 KB)
Uploaded: 07.06.2016
Positive responses: 0
Negative responses: 0
Sold: 1
Refunds: 0
Seller: Михаил_Перович
information about the seller and its items
Loyalty discount! If the total amount of your purchases from the seller more than:
| $1 | the discount is | 1% |
| $5 | the discount is | 2% |
| $10 | the discount is | 3% |
| $20 | the discount is | 5% |
| $50 | the discount is | 7% |
| $100 | the discount is | 10% |
| $200 | the discount is | 15% |
$0.63
Solution K3-28 (Figure K3.2 condition 8 SM Targ 1988)
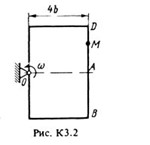
A rectangular plate (Figure K3.0-K3.5) or a circular plate of radius R = 60 cm (Fig. K3.6-K3.9) rotates about a fixed axis with a constant angular velocity ω given in Table. K3 (with a minus sign, the direction of ω is opposite to that shown in the figure). The axis of rotation in Fig. K3.0-K3.3 and K3.8, K3.9 is perpendicular to the plane of the plate and passes through the point O (the plate rotates in its plane); in Fig. K3.4-K3.7 axis of rotation OO1 lies in the plane of the plate (the plate rotates in space). On the plate along the straight line BD (Figure K3.0-K3.5) or along the circumference of the radius R, ie along the rim of the plate (Figure K3.6-K3.9), the point M moves. The law of its relative motion, expressed in the equation s = AM = f (t) (s - in centimeters, t - in seconds), is given in Table. K3 separately for Fig. K3.0-K3.5 and for Fig. K3.6-K3.9, while in Fig. 6-9 s = AM and is counted along the arc of the circle; b and l are given there. In all figures, the point M is shown in the position at which s = AM> 0 (for s <0 the point M is on the other side of point A). Determine the absolute velocity and absolute acceleration of point M at time t1 = 1 s.
A rectangular plate (Figure K3.0-K3.5) or a circular plate of radius R = 60 cm (Fig. K3.6-K3.9) rotates about a fixed axis with a constant angular velocity ω given in Table. K3 (with a minus sign, the direction of ω is opposite to that shown in the figure). The axis of rotation in Fig. K3.0-K3.3 and K3.8, K3.9 is perpendicular to the plane of the plate and passes through the point O (the plate rotates in its plane); in Fig. K3.4-K3.7 axis of rotation OO1 lies in the plane of the plate (the plate rotates in space). On the plate along the straight line BD (Figure K3.0-K3.5) or along the circumference of the radius R, ie along the rim of the plate (Figure K3.6-K3.9), the point M moves. The law of its relative motion, expressed in the equation s = AM = f (t) (s - in centimeters, t - in seconds), is given in Table. K3 separately for Fig. K3.0-K3.5 and for Fig. K3.6-K3.9, while in Fig. 6-9 s = AM and is counted along the arc of the circle; b and l are given there. In all figures, the point M is shown in the position at which s = AM> 0 (for s <0 the point M is on the other side of point A). Determine the absolute velocity and absolute acceleration of point M at time t1 = 1 s.
No feedback yet